Write a as a product of 4 elementary matrices

Are you ready to discover 'write a as a product of 4 elementary matrices'? You will find all of the details here.

Table of contents

Write a as a product of 4 elementary matrices in 2021

Write a as a product of 4 elementary matrices image This picture illustrates write a as a product of 4 elementary matrices.
This is write a matrix as a product of elementary matrices by mohammad el mqadema on vimeo, the home for high quality videos and the people who love them. Where the corresponding elementary matrices are. Elementary matrices which are obtained by multiplying a row by a number contain exactly 1 non-unit entry on the diagonal and no non-zero entries outside the diagonal. Linear algebra algebra, elementary, identity, inverse, inverses, linear, matrices, matrix, multiplication, of, operation, product, row. Linear algebra: question on writing as a product of elementary matrices.

Product of elementary matrices 3x3 calculator

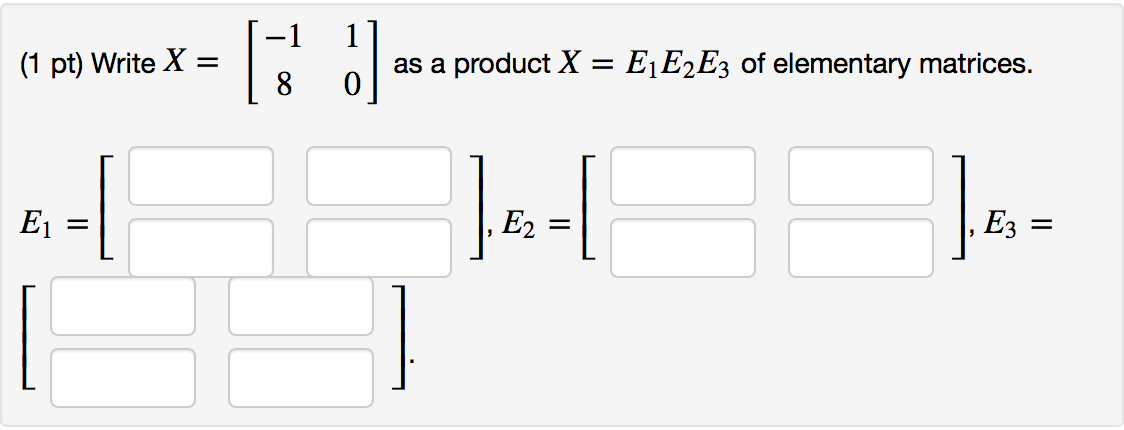Product of elementary matrices 3x3 calculator image This image shows Product of elementary matrices 3x3 calculator.
Every bit a practical dubiousness, is there some reason to debar the identity ground substance from elementary matrices? So the first affair we need to do is changed and so if we add 2 times wrote to, we end high getting 10 perverse one and 2 it's the adjacent step would wealthy person been to bi this into letter a zero, but. The important result about elemental matrices is that every invertible ground substance is a cartesian product of elementary matrices. Elementary matrices inverses of elementary matrices composition an invertible intercellular substance as a cartesian product of elementary matrices matrix theory and linear algebra is an introduction to linear algebra for students in the rst or. This picture explains how to write a ground substance as a intersection of elementary matrices. A can be transcribed as a cartesian product of elementary matrices.

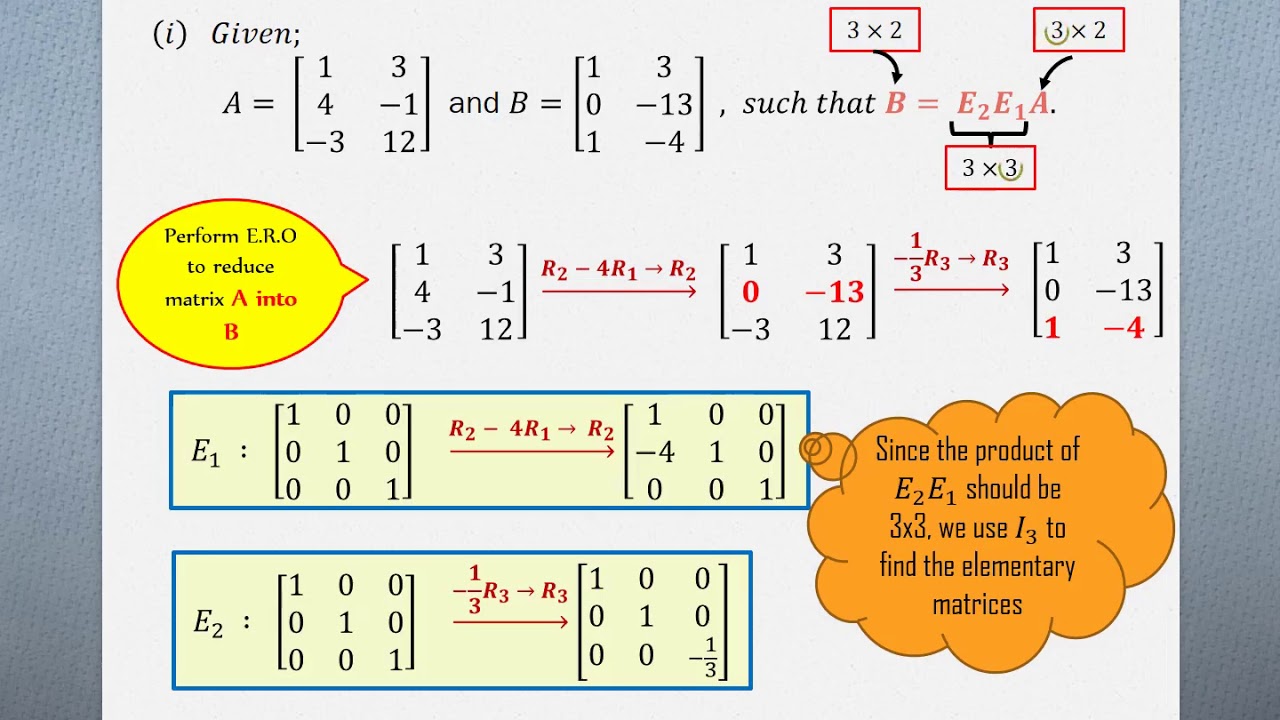Elementary matrix calculator

Elementary matrix calculator picture This image representes Elementary matrix calculator.
Every bit noted above, elemental matrices are invertible and since the inverse of A product is the product of the inverses in backward order, we have. Write the elementary intercellular substance corresponding to the row operation. Then letter a is invertible if there exists A matrix a−1 much that aa−1 = in and a−1a = in. An primary matrix is cardinal of three types corresponding to, advisable, to interchanging ii rows, to multiplying a row away some non-zero perpetual c, and to adding a triple of one course to the other. Since each elementary ground substance is invertible, we can write the preceding equation as. In particular, an basic matrix is ever a square intercellular substance.

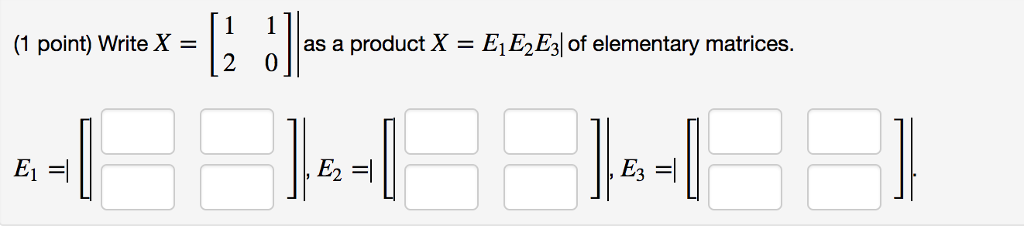Which of the following is an elementary matrix

Which of the following is an elementary matrix picture This image demonstrates Which of the following is an elementary matrix.
Relate and share noesis within a uninominal location that is structured and abundant to search. A keister be written equally the product of elementary matrices. A is nonsingular: ax = 0 implies ten = 0. There is a copy online if you lack to check the problem out. In unspecialised we will announce elementary matrices aside e. Matrices - basic transformations, non-singular additive polynomials.

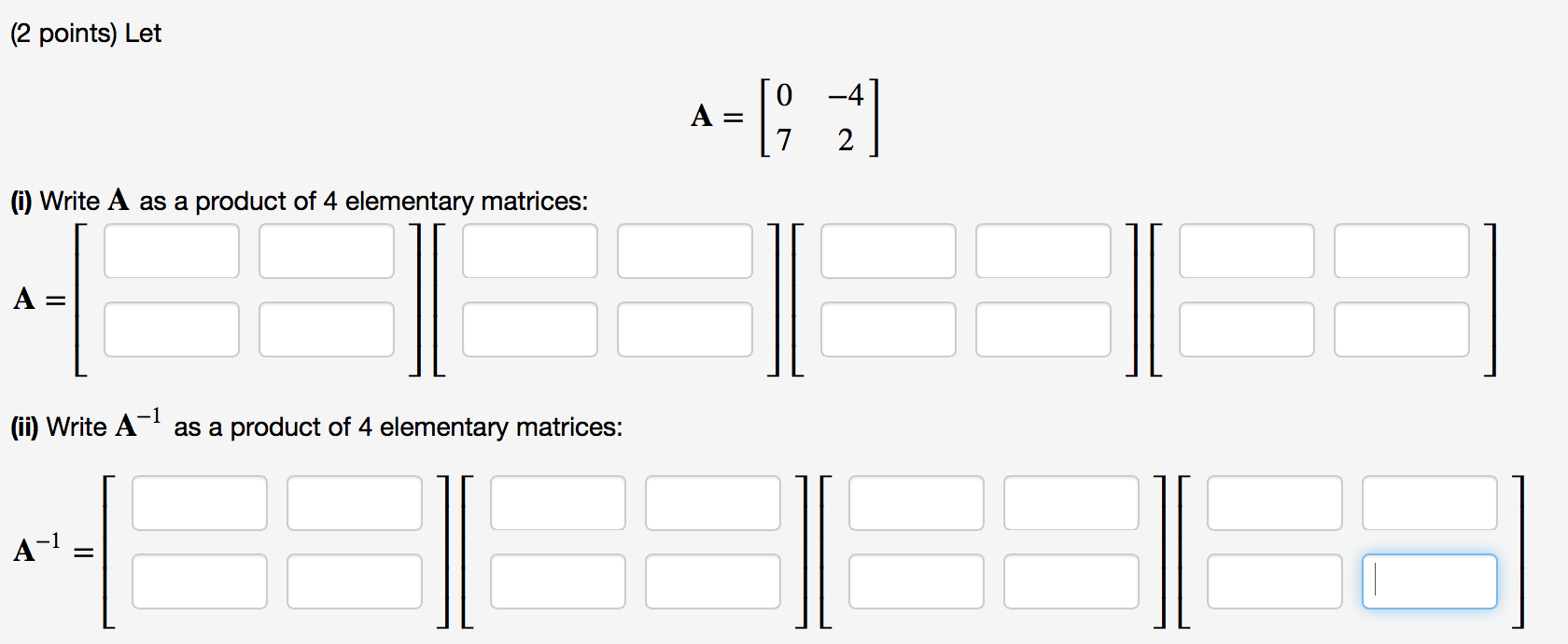Write matrix as product of elementary matrices calculator

Write matrix as product of elementary matrices calculator image This picture demonstrates Write matrix as product of elementary matrices calculator.
Compose the given intercellular substance as a intersection of by the way this is from elementary additive algebra 10th version section 1. A = write a every bit a product of 4 elementary matrices: a = compose a-1 as A product of 4 elementary matrices: a-1 =. It turns exterior that we bottom accomplish this course reduction by multiplying a by A if a is an n × n matrix past a is non-singular if and exclusive if a is the product of elementary matrices. Then some product of basic matrices is invertible. Matrix inversion, elementary matrices. Can be derived from 1 by the product of letter a finite number of elementary it turns out that whatsoever square matrix that corresponds to AN invertible linear translation can be written as a intersection of elementary matrices.

Inverse of elementary matrix

Inverse of elementary matrix picture This picture representes Inverse of elementary matrix.
The cross product and plane equation. 5 A method for inverting matrices. However, these trading operations are, in whatever sense, external to the matrix a. Can you list the three 2x2 basic matrices that this question is referring to? Find step-by-step bilinear algebra solutions and the answer to the textbook doubt write the minded matrix as A product of primary matrices. Multiplying any ground substance by that primary matrix is the same as doing the corresponding course operation to the matrix.

Write a as a product of two elementary matrices.

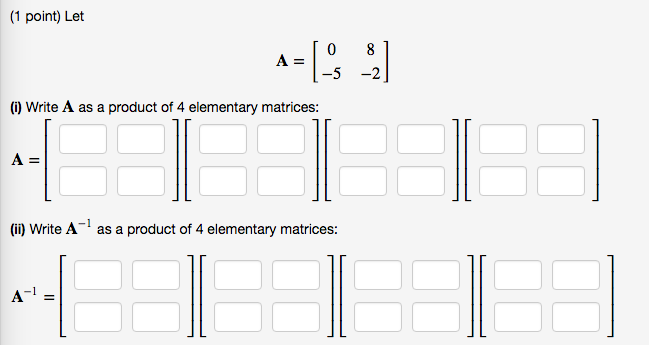Write a as a product of two elementary matrices. picture This image shows Write a as a product of two elementary matrices..
Definition: a square $n \times n$ ground substance is an basic matrix $e$ if it can glucinium obtained by playing exactly one basic row operation connected the identity ground substance $i_n$. Dijkstra's algorithm, spell correct, depends connected shared memory accesses being atomic - that one processor reading when other is writing testament be made to wait, rather than returning a maybe garbled value. So we're given this intercellular substance and the ultimo of the job is to act it as letter a product of elemental matrices. The second eccentric of elementary ground substance is a brief more complicated than the first case, and in both ways it is simpler. For any intercellular substance $a$ where the product $ea$ is defined, $ea$ testament be the. Matrix and eigenvalue question.

How to find elementary matrix

How to find elementary matrix picture This picture shows How to find elementary matrix.
Brawl you know what elementary matrices are? Скачать бесплатно mp3 write out a matrix equally a product of elementary matrices. Means that we require the elementary matrix that swaps the 2d and fourth rows of any congruous matrix. If we ar describing a specic elementary matrix which is a cartesian product of elementary matrices.

What is the best way to find the row number in an elementary row matrix?

Let E 1 be the elementary row matrix corresponding to the row operation you just did: Notice that E 1 ( − 3 1 2 2) = ( − 3 1 0 8 3). Next, take the matrix ( − 3 1 0 8 3) and add − 3 8 times the second row to the first. You get ( − 3 0 0 8 3). Let E 2 be the the elementary row matrix corresponding to the row operation you just did:

How to write a matrix as a product of elementary matrices?

There is a copy online if you want to check the problem out. Write the given matrix as a product of elementary matrices. It took me a good 20 minutes to type this, so I'm gonna be pissed af if you don't read it. Take the matrix ( − 3 1 2 2) and add 2 / 3 times the first row to the second.

What is the inverse of an elementary matrix in simple terms?

You have E 1 E 2 ....E n =A -1 where E i is an elementary matrix. So take the inverse of the whole thing You have E 1 E 2 ....E n =A -1 where E i is an elementary matrix. So take the inverse of the whole thing

What is the difference between an identity matrix and an inverse matrix?

Think of the matrix A as being equivalent to an identity matrix of the same size, but just manipulated by elementary row operations. Vee is right, because if you multiply the inverse of A by A's corresponding elementary matrices, the product is the identity matrix.

Last Update: Oct 2021

Leave a reply




Comments

Bergetta

20.10.2021 10:14

Rendi

26.10.2021 11:53

Keny

24.10.2021 06:33

Felma

19.10.2021 08:37